Compound interest has been called the eighth wonder of the world. We cannot verify whether that is true — we are pretty sure some governing body of the United Nations has to vote on that — but it’s a really good way to watch your money grow while doing nothing.
What is compound interest?
Simply stated, compound interest is the principle by which the interest you earn also earns interest, and the interest on that interest earns interest, ad infinitum. The larger your balance gets, the bigger those interest numbers become, thanks to exponential growth.
Compound interest generally applies to saving accounts and loans. You agree to borrow or save money over a set period and during that time interest is accumulated and compounded. Compound interest is also accumulated on a set frequency, whether that be daily, weekly, quarterly, or annually.
How does compound interest work?
Compounding is a popular concept when it comes to saving and investing because it's extremely helpful in calculating the future value of your savings. Plus, it's a pretty nice feeling to see how your money will be exponentially growing. The interest-on-interest effect can really generate some pretty delightful sums, especially if you're patient and keep contributing to your savings account. Since calculating compound interest can help you visualize the projected future value of your savings, it's a helpful tool for figuring out how long you need to save—and how much you have to contribute — in order to reach specific goals, like saving up for a deposit on your first house, or for a wedding.
Here's an example of how compounding can significantly grow your money. In this hypothetical example $10,000 is invested for three years at a return of 5.5% compounded annually. Each year the earnings grow due to compounding. At the end of the third year the principal sum is worth $11,742.41.
Year | Beginning of year value | Yearly Earnings | End of year value |
|---|---|---|---|
| 1 | $10,000 | $550 | $10,550 |
| 2 | $10,550 | $580.25 | $11,130.25 |
| 3 | $11,130.25 | $612.16 | $11,742.41 |
Compound interest doesn't just apply to savings and investment accounts, either. Cash accounts and certificates of deposit, like savings accounts, also work on the principle of compound interest. Assets like stocks, mutual funds, and exchange-traded funds also accrue interest, which is why investment accounts experience compound interest.
Things like loans—including mortgages — and credit cards also apply compound interest, that doesn't benefit you: in those cases, you accrue interest on your debt. And with credit cards, your debt has the capacity to quickly snowball out of control. Financial institutions like banks, robo-advisors, and brokerages allow you to collect compound interest.
As mentioned before, your money can be compounded on a daily, weekly, monthly, or yearly basis. The more often the money is compounded, the faster it grows. This is called the compounding frequency. A common way to quantify this and compare interest rates is with the annual equivalent rate (AER), a figure that shows what the annual rate on an account would be if interest was paid for a full year and compounded. Sometimes this is also referred to as the annual percentage yield (APY).
How to calculate compound interest
In the formula, "P" stands for principal amount, or present value. That’s the starting amount of your savings or the total value of a loan. The "i" represents the interest rate expressed as a decimal (5% = 0.05). "n" represents the number of times the interest is compounded each year, and "t" is the number of years the interest will be applied.
Confused? Fair enough. Here's how to work through it for a savings account with $15,000 that earns 5% annual interest for 30 years.
Interest earned = $15,000 (1 + .05/1)^1(30) – $15,000
Interest earned = $15,000 (1.05)^30 - $15,000
Interest earned = $15,000 (4.32) - $15,000
Interest earned = $64,800 - $15,000
Interest earned = $49,800
Not so bad.
Best compound interest calculators
If you want to skip the formulas and math there’s a variety of free online compound interest calculators you can use. The Ontario Securities Commission has free financial calculators on their site that will easily show you how your money will grow. All you need to do is put in your initial investment, your monthly contributions, the amount of years you intend to let your money grow, and the estimated annual interest rate.
Since compound interest is the main magical component that also helps retirement funds like Tax-Free Savings Accounts and Registered Retirement Savings Plans grow, it's helpful to use calculators for these accounts as well, in order to understand how much you can contribute for your savings to grow in the future.
Benefits of compound interest
The biggest benefit of compound interest is that you make a lot more money thanks to the “compounding” part. If you reinvested your returns on $10,000 over 30 years and earned 5.5% interest, you’d end up with nearly five times that thanks to the magic of compounding. Each year your balance increases, as do your returns. The money you’ve made — makes money. This snowball effect is a powerful way to build wealth over time. It’s also why you should resist withdrawing money from your savings and investment accounts and instead aim for a longer time horizon.
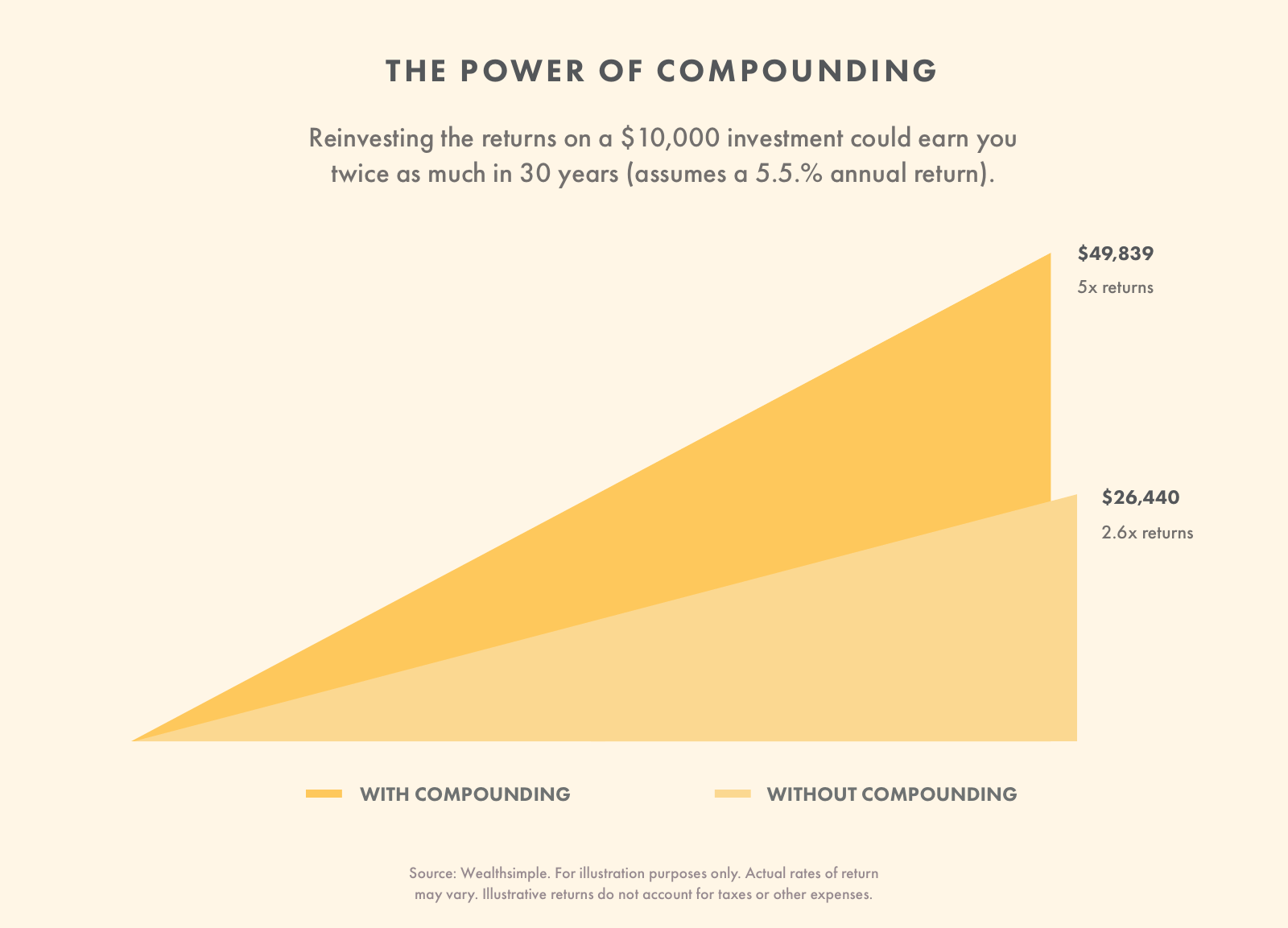
When you put money into an interest-earning account, the interest you receive each period gets added to your balance. Your new balance is used to calculate the next interest payment. Since your balance is getting bigger so too is the amount of interest you’re earning. If you use an automated investment portfolio, it’s best to make regular contributions and pretend the money doesn’t exist until retirement.
Every dollar you add to your balance creates a little more interest, and every bit of interest builds up your balance. This cycle is how many people become very wealthy. It may seem silly, but watching interest grow in a savings account or an investment product is captivating—your money increases without having to contribute any of your labor.
Compound interest is that it helps you reach your financial goals and prepare you for retirement or another savings goal. Stashing money under your mattress is technically saving for the future, but it doesn’t hold a candle to the power of a high-yield savings account or investment portfolio. Without compounding, you would have to work for every dollar of your nest egg.
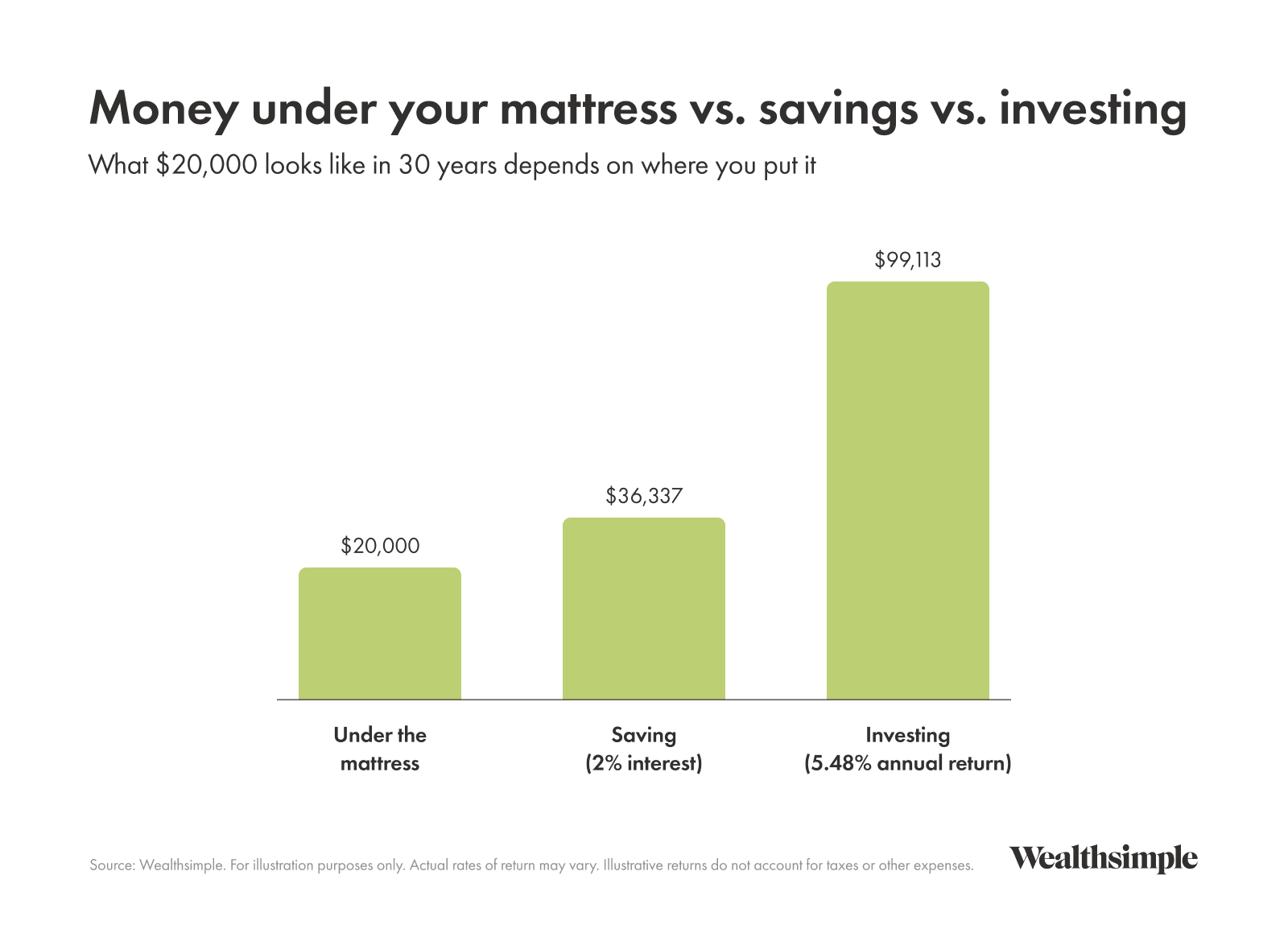
The earlier you start saving to benefit from the power of compounding, the more advantage you get. As the numbers get bigger, so does the benefit of compounding. Think of it like a snowflake turning into a giant snowball—the longer the hill is, the bigger the snowball can get.
Drawbacks of compound interest
Compound interest is rainbows and puppies when you are earning interest, but it’s whatever the opposite of rainbows and puppies is, if you owe money. As mentioned before, all that interest accumulating can quickly become a lead ring around your neck if it’s debt you’re accruing so exponentially. When it comes to compound interest in debt, the interest is hurting you, the borrower. Think about it: When you incur debt, you keep accumulating interest on that debt until the original debt plus the interest is paid off. And that interest keeps accumulating interest, which can quickly turn into a vicious cycle.
Credit cards are a great example of how compound interest can work against regular people. Assuming that you never pay your bill (which would never happen, right financially responsible people?), here’s what would happen:
Year 1: $10,000 + 20% interest = $12,000 ($2,000 in interest) Year 2: $12,000 + 20% interest = $14,400 ($2,400 in interest) Year 3: $14,400 + 20% interest = $17,280 ($2,880 in interest)
Within three years, the amount of money owed to the credit card company is almost double the original balance. That’s why it’s so important to always pay off your credit card balance in full. So to review: Compound interest is great if you’re earning, terrible if you’re owing.
Compound interest vs simple interest
While we’ve been talking a lot about compound interest, it’s important to understand the underlying foundation of that concept: simple interest. Simple interest refers to the interest that an initial sum accumulates over a period of time, but without the added component of calculating interest on the interest earned. Simple interest is determined by multiplying the daily interest rate by the original amount by the number of days that elapse between payments. This kind of interest is common for simple loans, and is usually measured with the Annual Percentage Rate, which displays the interest for a whole year.
Here’s how simple interest and compound interest compare. In this example you have $100 in the bank and your interest rate is 5% per year.
First, simple interest: Year 1: $100 + $5 = $105 ($5 in interest) Year 2: $105 + $5 = $110 ($5 in interest) Year 3: $110 + $5 = $115 ($5 in interest)
Now compare that to compound interest, with which the interest you earn also earns interest: Year 1: $100 + 5% = $105 ($5 in interest) Year 2: $105 + 5% = $110.25 ($5.25 in interest) Year 3: $110.25 + 5% = $115.76 ($5.51 in interest)
Compounding frequency
As mentioned before, the compounding frequency refers to the number of times per year (or per month, or per quarter, depending on the financial institution) that the accumulated interest is paid out, or credited to the account. The greater the compounding frequency, the more opportunity your money has to grow.
For example, if you invested $5,000 in an investment with a 5% interest rate, that money would grow much quicker if the interest was compounded monthly (you’d end up with $5,255 at the end of the first year) as opposed to annually (where you’d get $5,250). While this may not seem like a huge difference for one year, it’ll definitely add up as the years go by.
Continuous compound interest
So we’ve covered the difference between simple interest and compound interest. Now it’s time to introduce continuous compounding, the natural conclusion to what would happen if an interest rate just kept compounding without a deadline. Basically think of it as compounding on steroids. Instead of calculating for a certain number of years or months, you’re assuming a constant compounding over an infinite number of periods. While it’s not possible in practice, it’s an important theoretical concept in finance. If you’re ever so inclined, here’s the formula:
= P x e (i x t)
Wherein “e” stands for the mathematical constant approximated as 2.7183, “i” is the stated interest rate, and “t” is the time period, in years.
The law of 72
So let’s say you’re pretty happy with the rate of return you’re getting on your investment, and just out of pure curiosity you’d like to know how long it would take for you to double your money. Of course you could do a long calculation, or you could just use the handy Law of 72. This law says that the number 72, divided by the annual interest rate, is the amount of years it will take to double your money without ever contributing another cent! This Law is particularly handy if you’re trying to do some quick mental math to get an approximate value. It’s also very effective for very quickly visualizing the impact that compound interest can have.
So let’s say you have about $10,000 in investments, and you want to know how long it’ll take for you to double that money. If you have an interest rate of 5% (as in the example above), it would take you something like 14 years to double your money.


